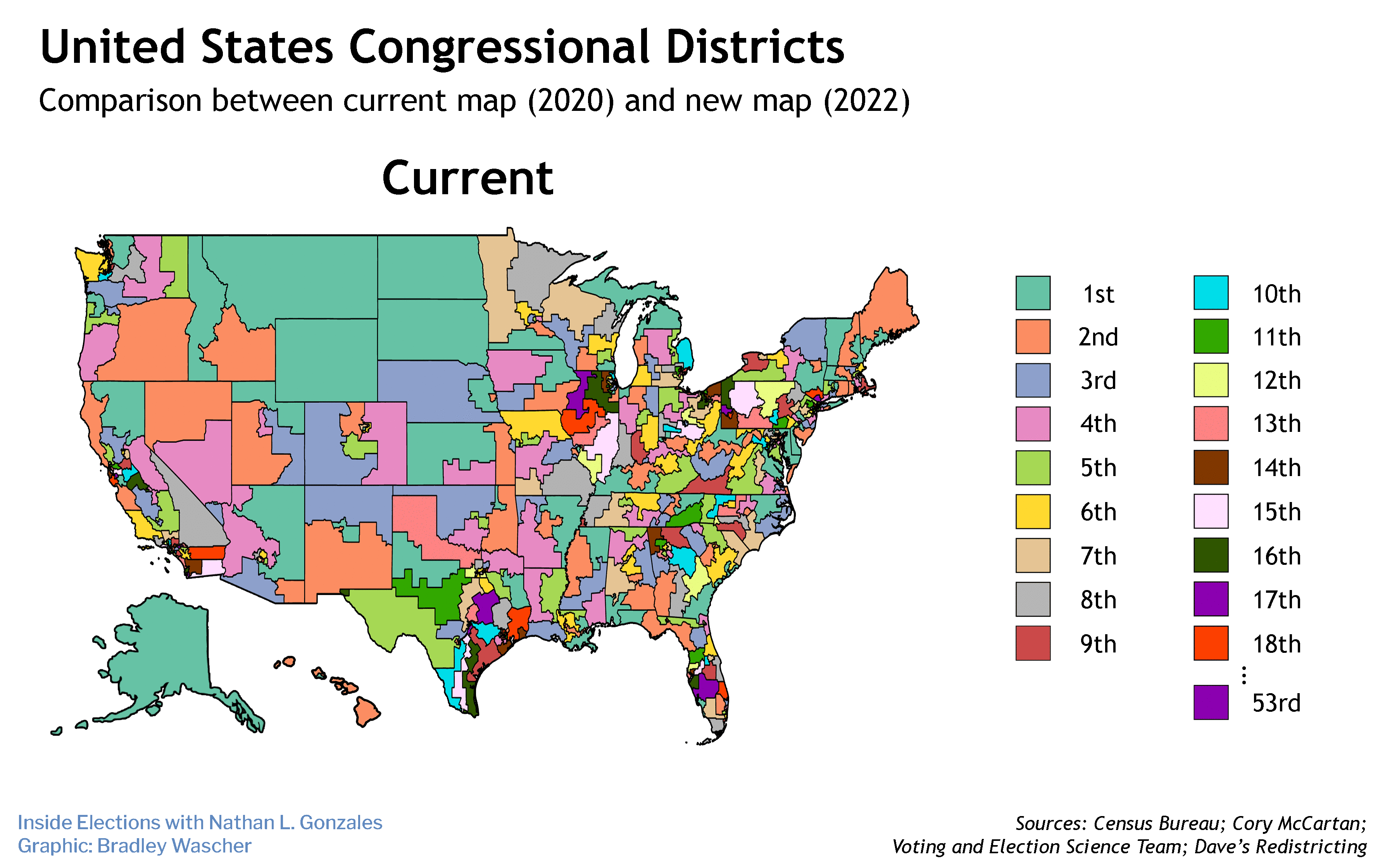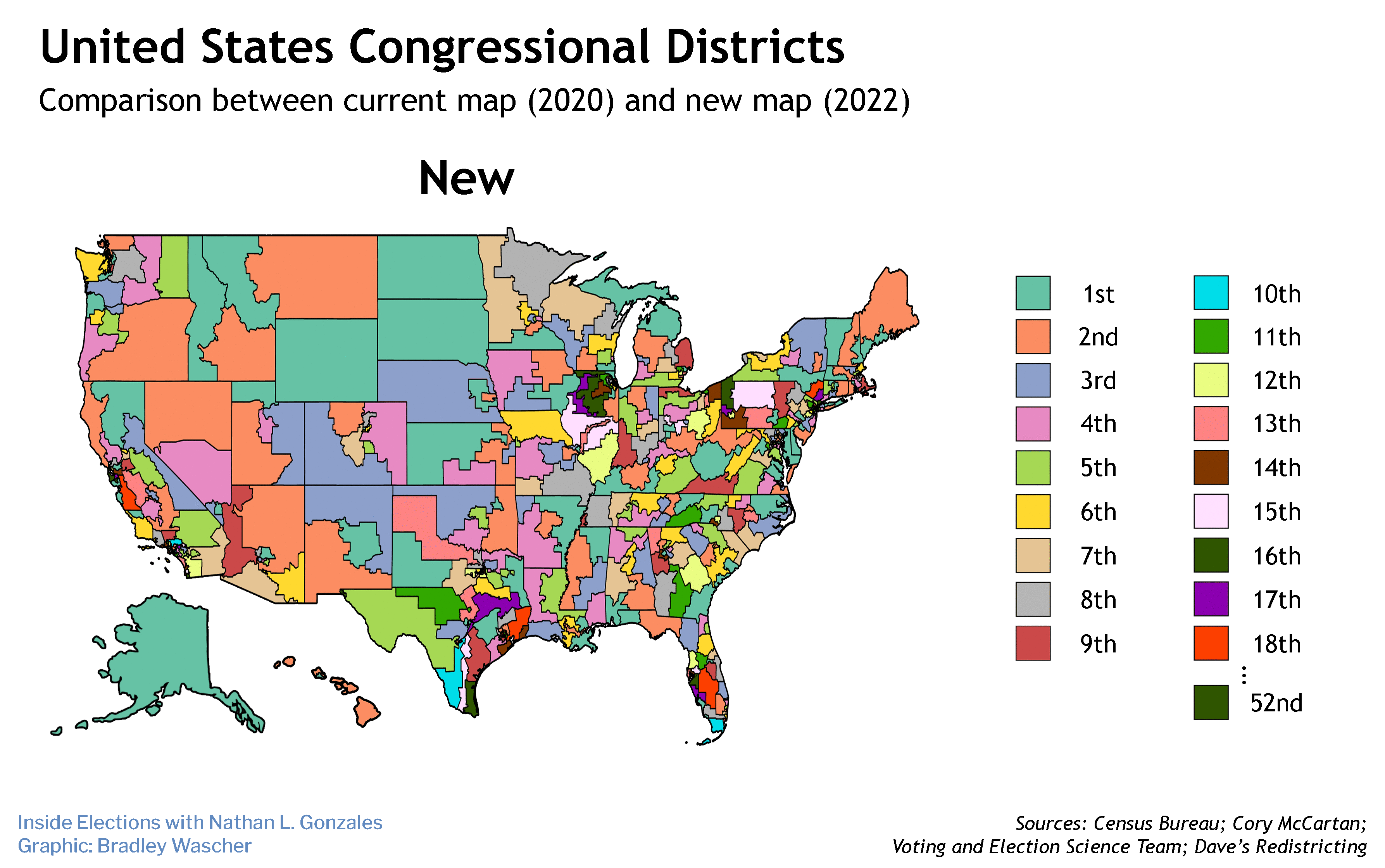
Campisi is an assistant professor of mathematics and statistics at San José State University and a Public Voices fellow with The OpEd Project, a nonprofit that promotes more diversity among thought leaders.
The systems by which we elect the president and House of Representatives are predicated in most people's minds by the idea of "one person, one vote." That simple idea is filtered though many political structures, however, and leaves different voters with different amounts of power. Proposals in Congress would give statehood, and full voices in the House and Senate, to both Puerto Rico and Washington, D.C. This would result in a shift in the amount of power held by the existing 50 states, members of our federal legislature and individual citizens.
In order to understand how changes like this dilute or concentrate our individual political power, it is critical to understand the mathematical concepts underlying our political systems.
The apportionment of representatives to states, the drawing of congressional district boundaries and how the preferences of voters are translated into the winner of an election are all examples of ways that math determines the influence of one person's vote.
Mathematics permeates our world and the systems of our society — yet it is often left out of public discourse. In order to empower the people to understand the systems which ultimately govern their lives, this must be remedied.
A lack of public mathematical discourse leaves open the possibility citizens will be convinced by incorrect or illogical arguments. Last December, for example, Donald Trump claimed it was "statistically impossible" for him to have lost the presidential election. By calling on a mathematical concept that many people feel uncomfortable with, Trump was able to bolster his claims of fraud and fuel the unrest that followed.
As someone who develops and analyzes mathematical tools to detect gerrymandering and also teaches undergraduates about the math of politics, I face this tension every day. I developed my Math in Politics course in an effort to open students' eyes to all the different ways math plays a role in the inner workings of politics at every level. Several universities have developed similar courses in recent years. I have been excited to see how understanding the math principles that quantify concepts such as "fairness" and "power" have driven students out of complacency about our political systems. Now they feel that they have authority to determine the legitimacy of an argument and therefore make stronger decisions.
Many have only recently become aware of the Electoral College and how it influences election outcomes. The number of electors for each state in 2024 and 2028 will be determined by the reapportionment of the House coming this spring, which will be decided by the population counts from last year's once-a-decade census.
This allocation of House seats is not the only way the power of a person's vote can be diluted or concentrated. Following reapportionment, 43 states will redraw their congressional districts. (The other seven will have small enough populations to merit one a single House member.) Because so much political power rests on the outcome of these maps, they are often drawn to entrench or expand political power — as opposed to in order to represent the will of the people.
Such partisan gerrymandering, the drawing of election maps in order to dilute the influence of one party's voters, is a major issue of our time. How exactly gerrymandering manifests itself has been a highly contentious issue.
Historically, irregularly shaped districts have been the first sign of a problem. Unfortunately, determining which shapes are unfairly "irregular" has been surprisingly difficult. Furthermore, modern mapmaking technology and fine-grained demographic data allow for the creation of highly partisan maps with "reasonable" shapes. For these reasons there is a need for tools to detect gerrymandering which do not rely on such an "eyeball test." Each state's geography, voter distribution and recent election results must be considered to paint a complete picture of whether a districting map is unduly partisan.
Several tools have been developed and tested in the courts in recent years. Some of the results of these cases however, have shown a disconnect between the level of mathematical sophistication necessary to capture gerrymandering and the level of mathematical comfort of the courts and citizenry.
In rejecting a 2018 Supreme Court challenge to Wisconsin's maps, for example, Chief Justice John Roberts characterized as "sociological gobbledygook" the plaintiffs' mathematical evidence that the lines were impermissibly partisan. Roberts went on to imply the average American would be unable to understand, or appreciate, a court decision based on math.
The point is not how the court decided the case, but that one of the most powerful people in the country said publicly that Americans wouldn't trust a court that used formulas to set legal precedent. He was right about the importance of citizens seeing the Supreme Court as deciding cases on legitimate grounds, of course, but wrong not to recognize the potential for sophisticated math to solve complex problems.
This attitude will work to the detriment of both the experts and lay people — because it will move both groups further from common ground. It also relegates a whole family of legal, moral and practical standards to the realm of not understandable and therefore not legitimate.
We have all heard many calls, during heated arguments, to defer to the experts. There is no question the pandemic has been made much worse by ignoring experts in favor of gut instinct, blind optimism and downright lies. It is not possible for each of us to develop the expertise needed to make fully informed decisions about everything.
There is a more nuanced approach. While deferring to the experts, make sure the experts — especially my fellow mathematicians — work to make their expertise is as accessible as possible. Math should be part of the public discourse. It should not be a black box to be avoided.